【CodeCraft 2019 华为软件精英挑战赛】城市交通动态系统最优配流问题
问题简述
问题定义
- 在模拟的道路图上为每一辆车规划行驶路线,系统会自动根据规划路线运行。
- 在路线合法的前提下,最终所有车辆按照规划的路线到达目的地。
- 系统调度时间短者胜出。系统调度时间指,从系统调度开始时间,至所有车辆全部到达目的地的时间,两者之差作为系统调度时间。
输入与输出
- 道路格式:(道路id, 道路长度, 最高限速, 车道数目, 起始点id, 终点id, 是否双向)
- 车辆格式:(车辆id, 始发地, 目的地, 最高速度, 出发时间, 优先级, 是否预置)
- 路口格式:(路口id, 道路id, 道路id, 道路id, 道路id)
- 预置车辆:(车辆id, 实际出发时间, 行驶路线序列)
- 输出:(车辆id, 实际出发时间, 行驶路线序列)
大致上来说,就是在一个有向连通图上,有很多辆车,从设定的起点出发,要到达预定的目的地,车辆按照一定的交通规则行驶,要求从系统执行调度的那一刻开始,到最后一辆车到达目的地的时间最短。官方给出了二十多页的文档详细描述了规则,详见官网文档。
问题分析
从问题的描述可知,这是一个动态系统最优(Dynamic System Optimal)的网络交通配流问题,即在一个有向连通图中,根据汽车的出发时间、起始点、目的点等交通需求,将汽车动态地分配到道路网络中的配流需求。在当前问题中,DSO 不考虑个体的最优,仅需要考虑从系统调度开始到所有车辆都到达目的地的时间最短。
大致可以有两条思路: - 事先规划道路并间隔发车(需要魔性调参) - 规划路线的优化 - 发车时间控制(车辆的发车顺序) - 编写判题器动态规划道路和发车时间(需要优化算法以控制程序运行时间) - 判题器执行的优化 - 寻路算法优化 - 死锁的解锁方法
出于对程序普适性的考量,这里采用结合判题器的发车时间设置。
最短路径规划
开始调度前,计算所有车辆对应的最短路径并保存。这里只能用单源最短路径(例如 Dijkstra 算法),因为每个车辆的速度是不同的,这里计算边的权重取: 1
边的权重 = 边的长度 / min(边的限速, 车速)
已知问题的输入规模为: > - 道路数据(226条道路) > - 路口数据(141个路口) > - 车辆列表(61440个车辆) > - 预置车辆(12151个预置车辆)
节点和边构成的图是一个稀疏图,采用邻接链表的方式进行组织。如果每个车辆单独计算最短路径,则需要计算 61440 次,通过适当的优化可以减少计算的次数。设每个节点出发的车辆车速均匀分布且有 m 种不同的车速,这样对于每个节点,均计算该节点出发到其他任意节点的每一个车速下的最短路径,则只需要计算 m * 226 次 Dijkstra 就可以算出所有车辆的最短路径。当车辆的车速 >= 边的限速时,车速不再影响边的权重,假设边的限速均匀分布,则可以进一步减少计算次数到 m / 2 * 226。而事实上不是每个节点都有车辆发出,并且有些节点的车辆车速分布数量小于 m,最终只需要计算大约一千五百次的 Dijkstra 就可以全部求出。
统计分析
- 下图是理论最优的最短路径长度分布,横坐标表示最短路径的距离,纵坐标表示最短路径为该距离的车辆数。由该图可知,最短路径的长度分布比较集中在,但是有少数车辆路径的长度较长,这部分车辆将延长调度时间。
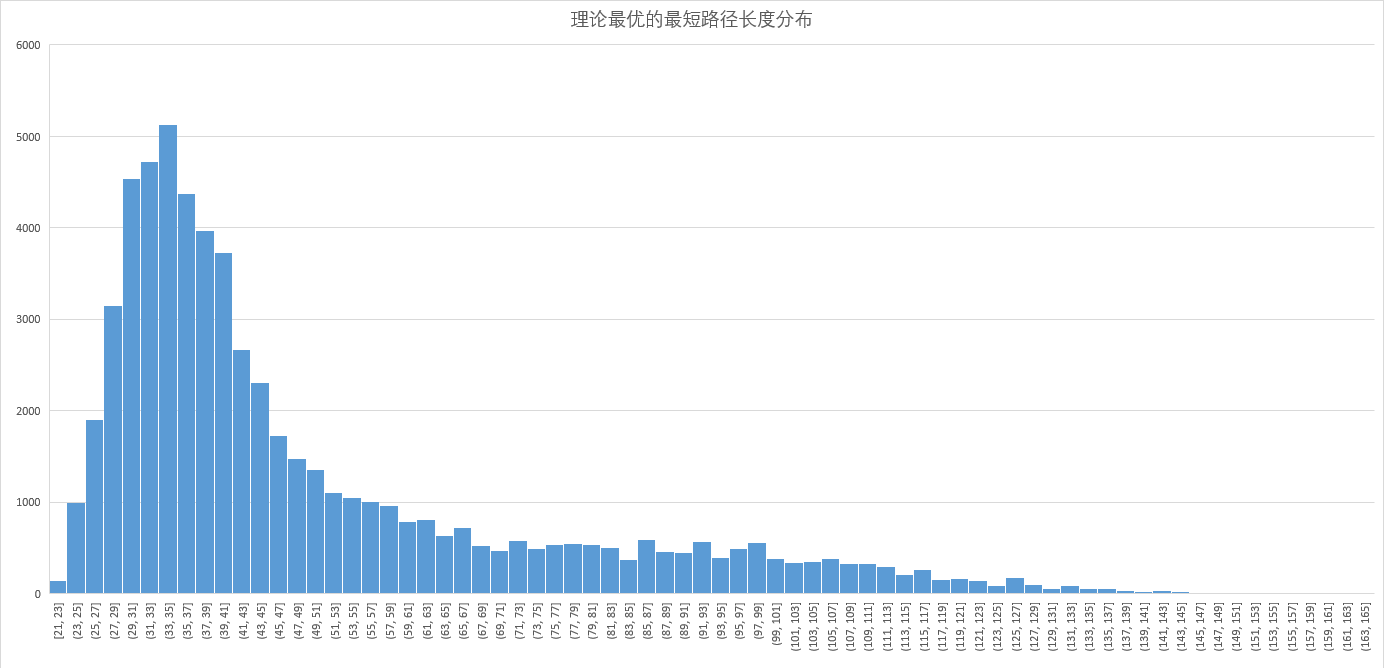
- 道路容量分布图,横坐标表示道路的容量值(道路长度 * 车道容量),纵坐标表示该容量的道路数。道路容量的分布也不是均匀的,有些道路容量较小,如果这些道路位于两个区域的核心枢纽上,将对调度产生很大的影响,如果能够以棋盘图的形式展现小容量道路在图中的位置,将会更加直观。
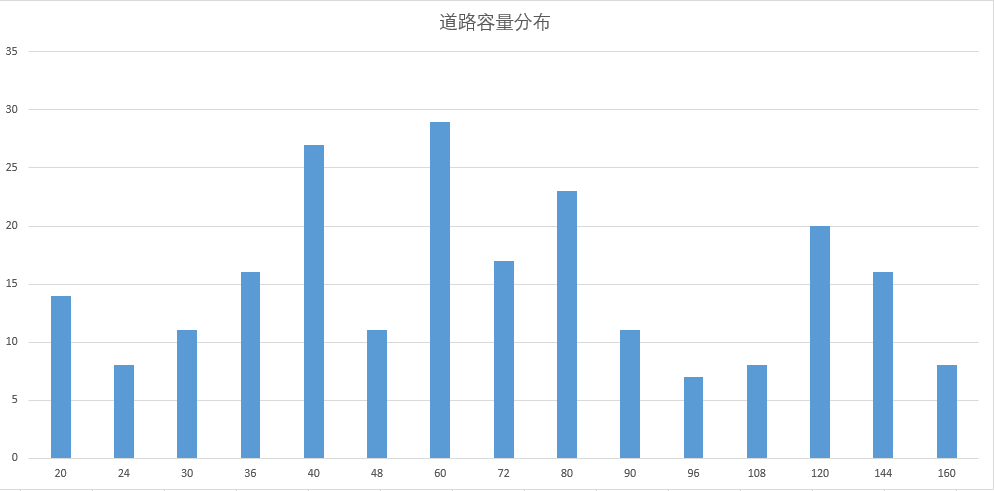
- 理论最优路径的道路通行车次分布,横坐标表示道路ID,纵坐标表示该道路对应通行的车次。虽然道路 ID 不连续,但也能反映出道路上通车的频次是不均衡的,有些道路的负载很高,有些道路的负载很低,高负载的道路是调度的瓶颈所在。

- 我们将道路ID映射到自然数N序列后,得到理论最优的最短路径长度分布,横坐标表示道路 ID,纵坐标表示该道路对应通行的车次,箱体为1。该图很直观地展现了道路的负载失衡,有个别道路的负载达到了 20000 以上,如果能够将最高负载降到 10000 左右,将是一个比较好的处理。
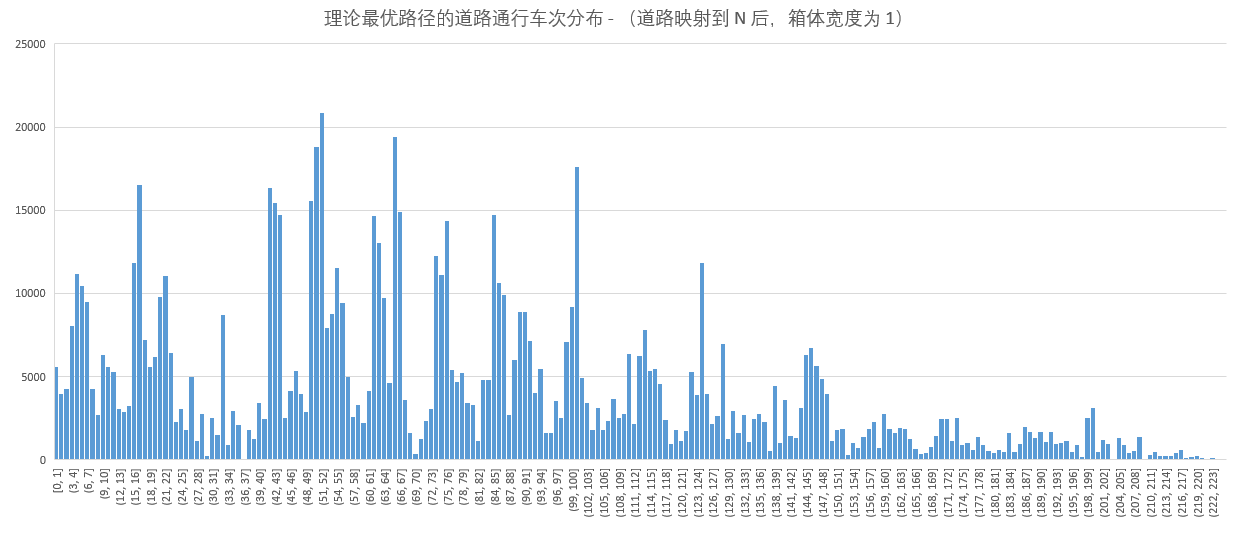
- 10000 辆车负载均衡后的道路通行车次分布,横坐标是各条道路,纵坐标是道路对应通行的车次。由图中可见,道路频数最高为 14000 多一点,通车频数超过 10000 的道路只有 6 条,这里负载均衡采用的边权重计算公式为:
1
边的权重 = (边的长度 / min(边的限速, 车速)) * 边的负载数 * 边的负载数

- 理论最优路径的道路通行车次分布散点图,横坐标表示车辆 ID 到 N 映射,纵坐标表示车辆对应的最短路径长度。
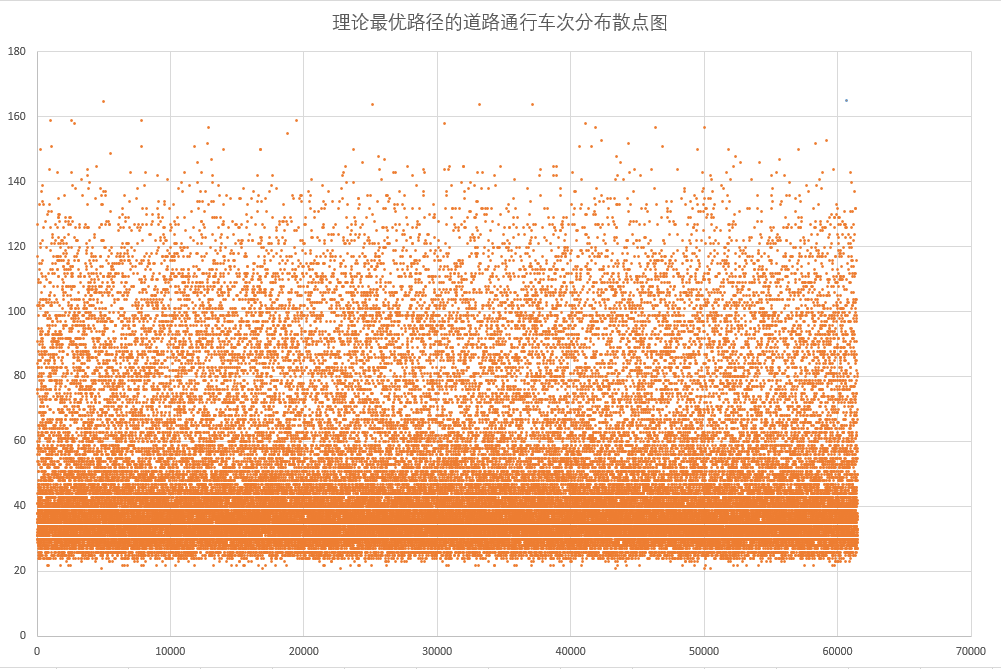
- 车辆出发点到目的点的分布,横坐标是出发点 ID,纵坐标是目的点 ID。节点 ID 和道路 ID 不连续真是深深的恶意....

- 我们将节点ID映射到自然数N序列后,得到下图,横坐标是出发点ID,纵坐标是目的点ID,散点透明度95%,黑色浓度越高,表示从同一个出发点到同一个目的点的车辆越多。从图中可以看出,有大量相同路线的车辆。

数据结构组织与判题器优化
Cross 类,组织了 Road 和 Car 的对象指针列表,Road 按照实际单行道组织到对应路口的进出口列表中。即如果一个道路是双向的,则该道路拥有两个 Road 实例,分别从点 from 到点 to 和从点 to 到点 from,并且分别组织到点 from 的 inner、outer、outer_sorted 和点 to 的 inner、outer、outer_sorted 中,这样可以通过指针快速地获取一个路口所有进出道路的实例。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Cross {
int id; // 路口 ID
int cntroads; // 路口道路数量
int orders[4]; // 路口道路序列,为空则值为 -1
int cntinner; // 进路口数量
int cntouter; // 出路口数量
Road* inner[4]; // 进路口序列,为空则值为 -1
Road* outer[4]; // 出路口序列,为空则值为 -1
std::vector<Road*> outer_sorted; // 出路口按道路 ID 排序的道路列表
std::vector<Car*> pri_cars; // 优先车辆队列,按照 [出发时间, 车辆 ID] 排序
std::vector<Car*> nonpri_cars; // 普通车辆队列,按照 [出发时间, 车辆 ID] 排序
std::vector<Car*> garage; // 该路口出发的所有车辆列表,无排序
std::set<int> speedset; // 该路口出发的所有车辆的车速集合
};Road 类
1
2
3
4
5
6
7
8
9
10
11
12class Road {
int id; // 道路 ID
int length; // 道路长度
int speed; // 限速
int channel; // 车道数
int from; // 源点
int to; // 目的点
int duplex; // 是否双向
std::vector<Car*> *next_roadway = nullptr; // 指向下一个车道的指针
std::vector<Car*> roadways[MAX_COUNT_ROADWAYS]; // 车道列表
};Car 类
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Car {
int id; // 车辆 ID
int from; // 出发点
int to; // 目的地
int speed; // 车速
int plantime; // 计划出发时间
int priority; // 优先级
int preset; // 是否预置
int status; // 车辆状态(终止态为当前时间点,等待状态为 -1)
int position; // 车辆在某条道路中的位置
int resched_on_cross; // 重新调度时所在的道路的出口节点
int resched_on_road; // 重新调度时所在的道路
int sched_plantime; // 调度计划的出发时间
int realtime; // 真实出发时间
int arrivedtime; // 抵达时间
std::queue<int> planpath; // 计划的车辆路径
std::queue<int> realpath; // 实际调度时走过的路径
};
根据判题器调度
一开始车辆没有实际出发时间,只根据计划出发时间分别排序到优先车辆队列和普通车辆队列中,调度的原则是: - 能上则上:只要路上有空位,就驱车上路 - 优先车优先:优先车辆优先上路 - 晚到达优先:尽可能让规划路线时得出的理论上最晚到达的车辆优先上路 - 较早到达的车辆的负载均衡:尽可能重新规划较早达到的非优先非预置车辆的路线,以达到道路负载均衡的目的
从第一个时间片开始,对每个路口,只要该路口满足上车的条件,则立刻尽可能多地将车辆派遣到道路上,直到遇到死锁。只要车辆上路,就更新车辆的实际出发时间以及实际出发路线。遇到死锁后就出发死锁解锁机制,同时进行路线的再规划。
死锁解锁的能力有限,为确保在死锁无法被解锁时,仍然能够重新规划出发时间和路线,每隔 5 个时间片就拷贝 Cross、Road、Car 的完整的备份,用于无法解锁时的数据回撤。
死锁的解锁以及路线的再规划
死锁的解锁即遇到死锁时,改变造成死锁的车辆的行车方向,使得死锁被解开。路口有行车方向优先级,解锁遵循如下原则,遍历所有造成死锁的车辆: - 如果造成死锁的车辆直行 - 判断能否左转,能左转时左转,并根据左转后的道路终点作为源点重新计算该车辆的最短路径; - 无法左转时,再判断能否右转,能右转时,根据右转后的道路终点作为源点重新计算该车辆的最短路径; - 如果造成死锁的车辆左转 - 判断能否右转,能右转时,并根据右转后的道路终点作为源点重新计算该车辆的最短路径; - 如果造成死锁的车辆右转,则跳过该车辆,处理下一辆
只要有一辆车辆能够被成功改变方向,则当前时间点的当前死锁即可被解除。但是仍然会存在所有死锁车辆均右转的情况。当死锁车辆均右转时,死锁无法被解除,则将造成死锁的车辆 ID 以及死锁发生的路口记录下来,并回撤到上一个存档点的位置(上面一节提到的每隔 5 个时间片就拷贝 Cross、Road、Car 的完整的备份,用于无法解锁时的数据回撤),重新规划被标记的车辆,修改部分车辆的右转为直行或左转,以避免全部右转造成无法解锁的死锁。
当车辆全部到达目的地时,调度完成,得到实际出发时间和实际行驶路线作为 answer.txt,解毕。
(完)
参考文献
[1] 孙瑜. 城市动态交通流分配模型与算法[D]. 2016. [2] 王中芳. 城市动态路网优化及交通流分配模型与算法研究[D]. 西安建筑科技大学, 2011. [3] 高自友, 任华玲. 城市动态交通流分配模型与算法[M]. 人民交通出版社, 2005.